23 April 2025
Speaker : Chris Hooley (Coventry) : Old and new physics in the J1-J2 Heisenberg spin chain
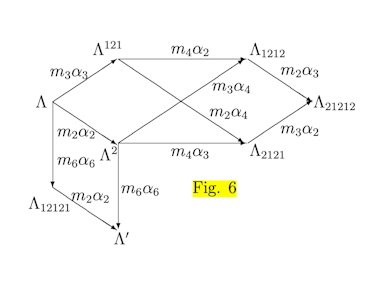
In this talk, I will briefly describe two of our recent pieces of work on the physics of the J1-J2 Heisenberg spin chain, a one-dimensional array of quantum spins coupled by first- and second-neighbour exchange interactions. The first piece of work [1] concerns the case where J1 and J2 are both antiferromagnetic: in this case there is a phase transition from a Luttinger liquid to a valence bond solid as J2/J1 is increased, and we provide a novel direct method to derive the field theory that describes the critical point between these two phases. The second piece [2] concerns the case where J1 is antiferromagnetic but J2 is strongly ferromagnetic: counter-intuitively, there is a transition in this case as well, but this time of a ‘liquid-to-liquid’ type. We present a field-theory description of it, and an analogue system of three coupled chains that helps to illustrate the physics.
14:00 - 15:30 in G.O. Jones Room 610